2023年上半年(高中数学)教师资格证面试试讲真题

　　2023年上半年(高中数学)教师资格证面试试讲真题

　　云南教资面试考试已经正式结束，云南教资报名网整理了2023年上半年(高中数学)教师资格证面试试讲真题，希望对大家有所帮助。

　　1.题目：《充分与必要条件》 2.内容：

　　3.基本要求: (1) 教学中注意师生间的交流互动，有适当的提问环节; (2) 要求配合教学内容有适当的板书设计; (3) 请在10分钟内完成试讲内容。

　　【答案解析】

　　【教学过程】(一)新课导入

　　给出两个命题，例如:(1)若x>a2-b2.则x>2ab;(2)若ab=0.则a=0.让学生判断两个命题的真假。由真命题出发，明确研究真命题中的条件和结论之间的关系《充分和必要条件》。

　　(二)新知探索

　　给出充分条件和必要条件的定义。

　　一般地,“若p,则q”为真命题，是指由p通过推理可以得出:q。这时我们就说,由p推出q，可推出p=q，记作并且说p是q的充分条件，q是p的必要条件。

　　强调命题中的条件和结论。

　　提问学生命题(1)是真命题，是否能解释一下命题((1)中p和q之间的关系。学生能够用概念直接进行解释。

　　让学生通过小组讨论的方式进行探究：除了利用定义解释，能否利用原命题的逆否命题进行解释呢?强调可以互为逆否命题同真假的这个结论进行解题。

　　(三)课堂练习

　　问题:下面“若p，则q”形式的命题中，p和q之间的关系是什么?若x=1.则x2-4x-3 =0;

　　(四)小结作业

　　小结采用发散性问题：你今天有什么收获?

　　作业：像刚刚解决的问题，如果p→q并且q→p，那么p，q之间又是什么关系呢?

　　【板书设计】

　　充分和必要条件

　　定义：

　　例题：

　　1.题目：《双曲线的标准方程》 2.内容：

　　3.基本要求: (1)试讲在10分钟之内完成; (2)讲解要目的明确、条理清楚、重点突出; (3)根据讲解的需要适当板书与作图; (4)引导学生类比椭圆的标准方程推导双曲舶的标准方程。

　　【答案解析】

　　(一)导入新课

　　带领学生复习双曲线的定义：平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线。这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。说明这节课将学习双曲线的标准方程。

　　(二)讲解新知

　　组织学生类比椭圆的相关知识，建立合适的平面直角坐标系，明确：设点F1、F2所在直线为轴，它们的中点为坐标原点，则”轴为线段F1F2的垂直平分线。设点M(X, Y)是双曲线上任一点，F1(-c, 0),F2(c, 0)。

　　再请学生类比椭圆标准方程的推导过程,探究双曲线标准方程的推导过程。组织学生小组讨论，教师巡视指导。

　　根据学生的经验，学生能够完成推导过程，教师板书并规范步骤。

　　教师讲解：从上述过程可以看到，双曲线上任意一点的坐标都满足方程①。以方程1的解(x,y)为坐标的点到双曲线的两个焦点F1(-c,0) ,F2(c，0)的距离之差的绝对值为2a，即以方程①的解为坐标的点都在双曲线上。由曲线与方程的关系可知，方程①是双曲线的方程，我们把它叫做双曲线的标准方程。它表示焦点在x轴上，焦点分别是F1(-c,0) ,F2(c，0)的双曲线，这里c2=a2+b2.

　　1.题目：等比数列前n项和公式的应用 2.内容：

　　3.基本要求： (1)试讲时间10分钟以内; (2)讲解要目的明确、条理清楚、重点突出; (3)根据讲解的需要适当板书; (4)分析解决问题的思路，指导学生正确应用等比数列的前n项和公式。

　　【答案解析】

　　(一)导入情境

　　创建一个情境，题为“国王给国际象棋队发明者的奖励”。假设一千粒小麦的质量为40克，并以目前世界上约60亿吨小麦的年产量为基础。

　　并询问学生是否认为国王能够满足他的要求，如何计算?请列出配方。

　　例2.某商场今年销售计算机5000台，如果平均每年的销售量比上一年的销售量增加10%，那么从今年起，大约几年可使总销售量达到30000台(结果保留到个位)?

　　(五)小结作业

　　提问学生，试着让学生总结本节课所学内容，老师适当补充。

　　本节课的小结从以下几个方面进行：

　　(1)等比数列的前n项和公式;

　　(2)公式的推导方法——错位相减法。

　　作业：思考分析等比数列与等差数列在研究过程中有什么相似之处。

　　四、板书设计

　　1、题目：高中数学《平面与平面的位置关系》

　　2、内容：

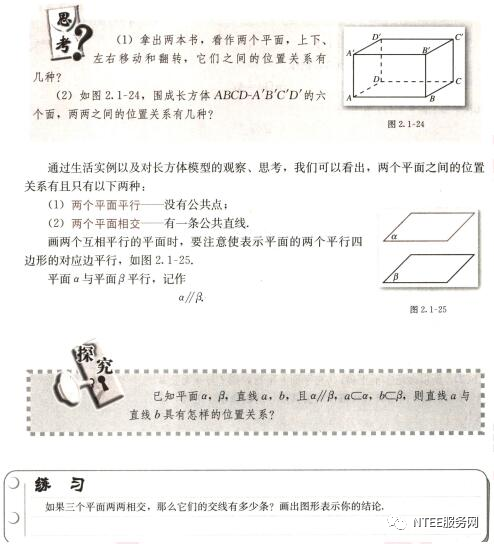
　　3、基本要求：

　　(1)如果教学期间需要其他辅助教学工具，进行演示即可

　　(2)让学生结合生活实例理解平面与平面的位置关系

　　(3)教学中注意师生间的交流互动，有适当的提问环节，突出学生的学习主体地位

　　(4)要求配合教学内容有适当的板书设计。

　　(5)请在10分钟内完成试讲内容。

　　【答案解析】

　　(一)导入新知

　　回顾直线与直线、直线与平面的位置关系。提问：平面与平面的位置关系又是如何的呢?

　　引出课题——平面与平面的位置关系。

　　(二)探索新知

　　活动一：学生自主尝试，拿出两本书，看做两个平面，上下、 左右移动和翻转，观察它

　　们之间的位置关系有几种。

　　活动二：教师出示长方体ABCD-A'B'C'D' ，学生思考围成长方体的六个面两两之间的位置关系有几种。

　　预设：两种，有公共点和没有公共点。

　　追问：如果两个平面有公共点，那么这些公共点形成了什么样的图形?

　　预设：根据公理3.这些公共点在一条直线上。

　　根据学生的回答，教师总结平面与平面的位置关系:两个平面有一条公共直线，我们称两个平面相交;两个平面没有公共点，则称两个平面平行。

　　教师强调：画两个互相平行的平面时，要注意使表示平面的两个平行四边形的对应边平行。平面α和平面β平行，可记作α∥β。

　　学生自主尝试用图形表示平面与平面的位置关系。

　　组织学生四人为一小组，十分钟的时间进行讨论，已知平面α，β直线a，b，且α∥β，a⊂α，b⊂β，则直线a和直线b具有怎样的位置关系，再请小组代表发言自己小组的讨论结果。

　　预设：平行或异面。

　　(三)课堂练习

　　如果三个平面两两相交，那么它们的交线有多少条?画出图形表示你的结论。

　　(四)小结作业

　　提问：今天有什么收获?引导学生回顾平面与平面的位置关系。

　　课后作业：练习题目。

　　【板书设计】略

　　1.题目:弧度与角度的转化

　　2.内容:

　　3.基本要求:

　　(1）要有板书﹔

　　(2）条理清晰，重点突出;

　　(3）教学过程注意启发引导;

　　(4）学生掌握弧度与角度的转化方法。

　　【答案解析】

　　(一)导入新课

　　问题1：我们已经知道角的度量单位是度、分、秒，它们的进率是60.角是否可以用其他单位度量呢?是否可以采用10进制?

　　问题2：角的弧度制是如何引入的?为什么要引入弧度制，好处是什么?角度制与弧度制的区别与联系?

　　(四)小结归纳，布置作业

　　小结：本节课你有哪些收获

　　作业：同桌互相给出角度或者弧度，另一个人进行转化。

　　【板书设计】略

　　以上就是关于2023年上半年(高中数学)教师资格证面试试讲真题的全部内容，考生如果想获得更多关于云南教师资格证相关资讯，如云南教师资格证考试内容、云南教师资格证面试、云南教师资格证成绩查询以及相关知识，敬请关注我们云南教师资格网。